Intro
这篇文章发表在 ICLR 2018 wordshop 上,文章总共只有四页,基本上属于讨论性质。在文章中,作者给 Dynamic Routing 做出了设想,认为其是在优化一个 聚类loss + KL 散度,并据此优化问题给出了一个自己的理论上更合理的解,在实验中初步证明了修改过的 Routing 算法效果更好。
Method
Dynamic Routing 的一种理解
首先为了方便起见,我们将 Dynamic Routing 的算法挂在下面

作者认为这段算法本质上是在做下面的优化问题
这里 $C = \{c_{ij}\}$ , $S = \{s_{j}\}$ 分别为 Routing 得到的权重以及 j 层的 capsule 值
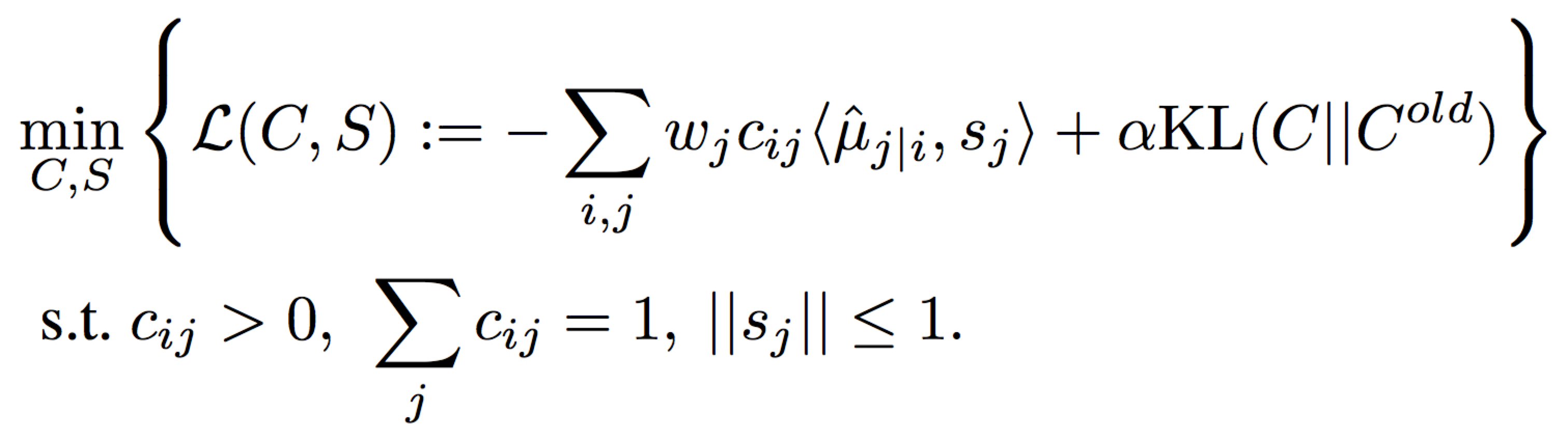
对应这个优化问题,我们来看算法1:
- line 4: 固定 $C$, 优化 $S$
- line 3 和 line 5: 固定 $S$ , 优化 $C$
P.S. 我觉得这里只能说是宏观上对应,作者也说了这个解释有着没有给 Squashing 函数留空间等等局限性
Author’s work
作者进一步提出了一个新的优化目标,并据此给出了算法
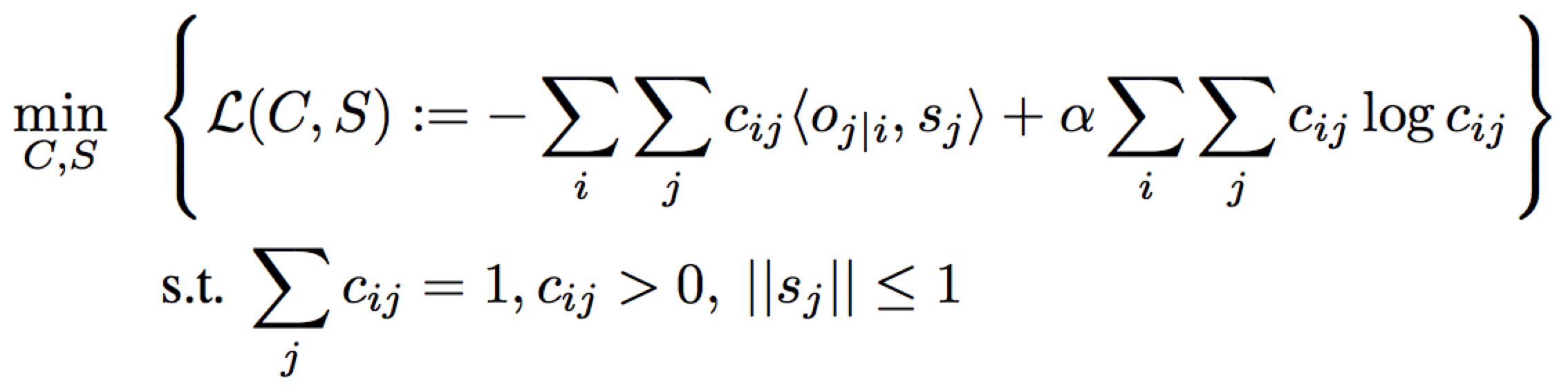
这里 $o_{j|i} = \frac{1}{\parallel{}T_{ij}\parallel{}_{\mathcal{F}}}T_{ij}\mu_{i}$,$\parallel{}T_{ij}\parallel{}_{\mathcal{F}}$ 是 $T_{ij}$ 的 Frobenius 范数(即各项元素平方值总和)

思考
- 文中给出的优化目标已经明确了Routing过程就是一个聚类的过程。当然也有可能反过来,作者先明确聚类本质,然后对此给出了优化目标并与算法进行对应。