Hinton团队出品的 Capsule 相关文章有三篇,按时间顺序排列为
- Transforming Auto-encoders
- Dynamic Routing Between Capsules
- Matrix Capsules with EM Routing
Transforming Auto-encoders
注:这篇文章年代较早,没有仔细阅读其中的技术细节。
Intro
CNN 做的事情是通过局部的参数共享减少参数数量,并通过 pooling 机制来进行下采样,从而实现局部平移的不变性 (local translational invariance)。
Hinton 等认为这一做法是不妥当的。CNN 得到的是一系列局部的标量激活值,而真正应该做的是用局部 “胶囊” (Capsules)来表征特征。这里提出的 Capsule 概念与之后的 Capsule 概念有一定的不同,它是一系列复杂的内部计算的组合。(这时的 Capsule 长相像是一个真正的胶囊,而后来的 Capsule 的概念更像是这时的 Capsule 单元的输出,是一个向量。)Capsule 学习到的是一个隐式定义的实体,它同时输出该实体的概率值和一些“实例化参数”(instantiation parameters)如姿态、光照、形变等等。
Capsule 的输出同时具有不变性 (invariant) 和同变性(equivariant)。局部实体变化时,其概率值不变,但实例化参数改变。
Capsule 这样显式输出实例化参数的好处是便于去做 “部分-整体” 的预测。若已有两个低层 Capsule $T_{A}$ 和 $T_{B}$,我们想要推测高层 Capsule $T_C$(即根据A和B推测C的存在性),可以使用坐标变换矩阵 $T_{AC}$ 来通过 A 对 $T_C$ 得到一个预测,同样可以通过 B 和 $T_{BC}$ 对 $T_C$ 做一个预测,若两个预测一致,则可以说 A 和 B 能够以正确的空间关系激活 C。
举例来说:假设 A 是嘴巴,B 是鼻子,C是脸。那么嘴巴和鼻子相对脸的位置应该是一定的,可以用 $T_{AC}$ 和 $T_{BC}$ 来表示,那么通过嘴巴可以推测出脸的一个描述 $T_{A} \times T_{AC}$,这个描述不仅说明了可能有人脸出现,同时还包括了人脸的实例化参数(如图中的位置、角度等);同样鼻子也能得到另一个推测。若这两个推测高度吻合,则能说明图中确实有一张正确的脸;(下图左)否则它们会出现冲突,模型也能正确推断出这不是一张正确的人脸。(下图右)
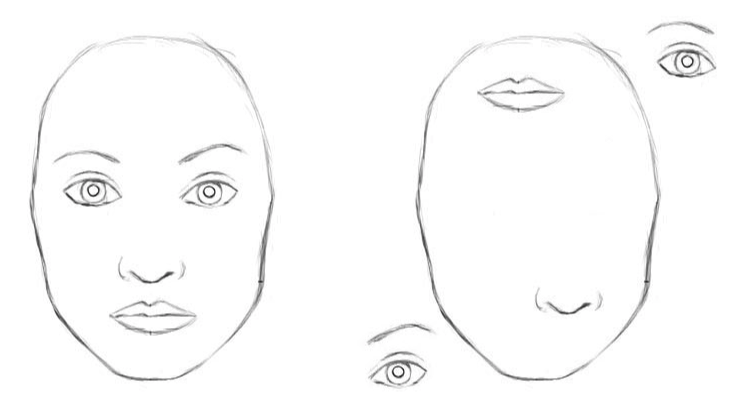
注意在”部分-整体”推测中仍然有着不变性和同变性。”部分-整体” 关系是不变的,以权重矩阵表示;观测到的部分(A和B) 和目标(C)的部分实例化参数是同变的,通过激活来表示。
Summary
这篇文章提出了 Capsule 的概念,确实让人耳目一新。我最开始接触 CNN 时,就对其一系列卷积和池化的操作很不理解,觉得漏掉了很多信息。通过 Capsule 来建模,能够更好的利用局部-全局的位置等信息,看上去是一个非常直观又有道理的想法。
文中使用 Transforming Auto-encoders 来对胶囊机制进行训练,基本想法是通过学习平移图片来约束胶囊内部的各个权重学习到 pose parameters,有些像 Dynamic Routing Between Capsules 中的 Reconstruction。(当然本质思想大概都是 auto-encoders 的变种)
由于年代久远没有我们熟悉的MNIST等实验结果。看到知乎上有一个描述感觉很精髓:
传统的CNN是这样理解的:人脸 = 一张鼻子 + 一个嘴巴 + 两只眼睛,但在识别毕加索图画时候,CNN会犯错的;
所以Hinton看来,应该是这样进行特征理解的:人脸 = 两个相邻的眼睛 + 眼睛下有嘴巴和鼻子。
Dynamic Routing Between Capsules
Intro
这篇文章简单来说有两个重要的思想:
Capsule
一个 Capsule 是一批神经元的集合,以向量形式表示,对应传统神经网络中的神经元。将 “scalar in scalar out” 变成了 “vector in vector out”。
每一个 Capsule 可以认为标定了一个隐性的实体,Capsule 向量的模长描述该实体出现的概率,向量方向作为实例化参数(instantiation parameters)。如果说神经元只可以描述为”有没有”某一个特征,那么 Capsule 除此之外还可以描述”有怎样”的特征。
Dynamic Routing
可以认为是对应上一篇论文中 “部分-整体” 预测的另一种具体实现。类似CNN,高层的 Capsule 单元被认为具有更大的感受野(receptive field),表示更加整体的实体。
通过一个转移矩阵来描述低层 Capsule 与高层 Capsule 的关系,我们可以得到对高层 Capsule 的几个预测,若这些预测高度吻合(agreement),则可以激活对应的上层 Capsule。(如有鼻子有眼则认为是一张脸)
也可以从特征提取的角度考虑,通过对低层 Capsule 进行变换得到特征空间,并在特征空间中进行聚类,找到特征密集点,作为上层的特征描述。
Method
视角不变矩阵
采用权重矩阵对低层 Capsule 进行变换,这一步可以看作是从低层 Capsule 推测高层 Capsule 的部分实例化参数。另一个角度来说,若没有这个变换,多层 Capsule 提取到的特征其实都是直接从第一层 Capsule 加权得到(顶多加一个 squash)。
Dynamic Routing
line2: 初始化,所有低层 Capsule 分配的权值一样
line5: 在当前权值下找到聚类中心
line6: squash类似于神经网络中的激活函数,是非线性函数,其将 $s_j$ 约束到 [0,1)
line7: 重新计算各个向量 $\hat{u}_{j|i}$ 与 $v_j$ 的距离,距离越近的权值越大
一般这里做三轮迭代,若迭代次数过多可能会加大泛化误差
CapsNet
这里有来自 Mike Ross 的一张解析图,我觉得讲的很清楚
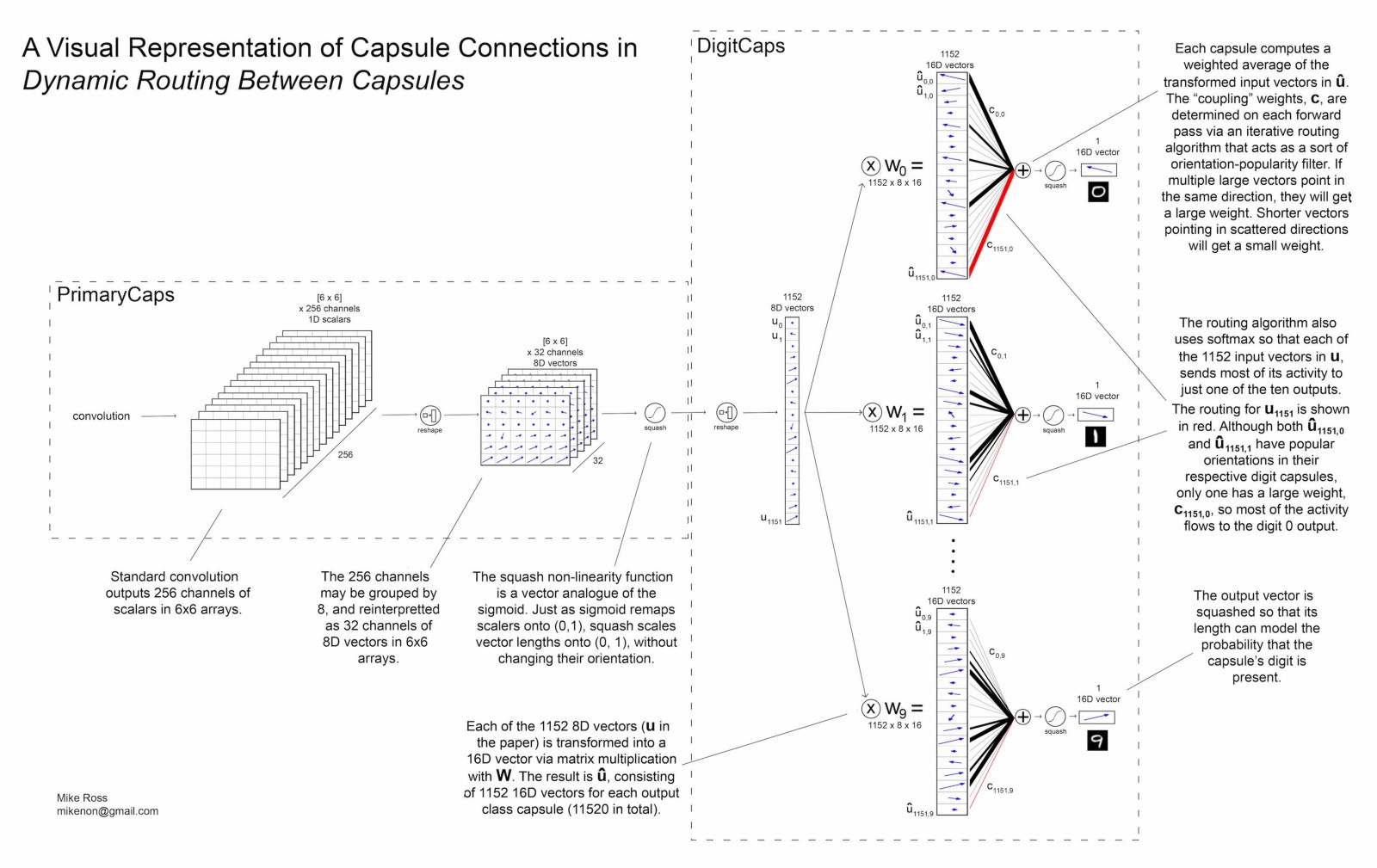
Reconstruction
我认为这里是上一篇 Transforming Auto-encoders 的思想的延续。使用这种重构的方法,作者认为属于一种 Regularization,可以更好的约束 Capsules 去学习实例化参数。
Experiment
MNIST
在MNIST上取得了SOTA的效果,并且表现出很好的对图片仿射变换的鲁棒性。
针对最后的 DigitCaps 中的每个维度进行扰动,发现这里每个维度似乎确实能够学到一些特定的实例化参数。
MultiMNIST
MultiMNIST 是 MNIST 的一个变种,它的每一张图片都包括两个高度重叠的手写数字。CapsNet在这个任务上显著优于CNN。
其他数据集
CIFAR10 上 10.6% 的误差,不是非常理想。
smallNORB 上 2.7% 的误差,接近SOTA。
Summary
比较成熟的Capsule概念,以及可行的Routing方法。并且取得了非常有趣的实验效果,说服力还是不错的。
主要有几个问题。
- 为什么仅需要三次迭代就能达到这样的效果?后续有研究甚至说两次迭代就能得到最好的结果(Pushing the Limits of Capsule Networks),为什么会这么快?
- 不易处理复杂问题。在 Capsule Network Performance on Complex Data 中,论文作者尝试了多层、ensemble等等,发现在 CIFAR10 上效果都不是非常好。另外,由于过程中的迭代过程,训练效率必然不会太高。
Matrix Capsules with EM Routing
未完待续